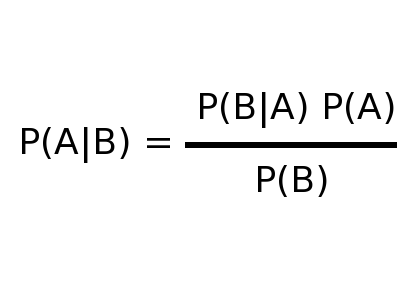 Bates theorem is named after the Rev. Thomas Bayes (1701–1761), who first formulated it. It is essentially a statistical tool that allows you to work out the probability of something.
Bates theorem is named after the Rev. Thomas Bayes (1701–1761), who first formulated it. It is essentially a statistical tool that allows you to work out the probability of something.
The Cancer Illustration
Let’s quickly illustrate how it works. If you wanted to work out the probability that somebody has cancer and you knew how old they were then you could use the information you have, their age, to determine the cancer probability.
The Wikipedia on it all article covers this example …
Suppose we want to know an individual’s probability of having cancer, but we know nothing about them. Despite not knowing anything about that person, a probability can be assigned based on the general prevalence of cancer. For the sake of this example, suppose it is 1%. This is known as the base rate or prior probability of having cancer. “Prior” refers to the time before being informed about the particular case at hand.
Next, suppose we find out that person is 65 years old. If we assume that cancer and age are related, this new piece of information can be used to better assess that person’s risk of having cancer. More precisely, we’d like to know the probability that a person has cancer when it is known that they are 65 years old. This quantity is known as the current probability, where “current” refers to the theorised situation upon finding out information about the particular case at hand.
In order to apply knowledge of that person’s age in conjunction with Bayes’ Theorem, two additional pieces of information are needed. Note, however, that the additional information is not specific to that person. The needed information is as follows:
- The probability of being 65 years old. Suppose it is 0.2%
- The probability that a person with cancer is 65 years old. Suppose it is 0.5%. Note that this is greater than the probability of being 65 years old. This reflects that people with cancer are disproportionately 65 years old.
Knowing this, along with the base rate, we can calculate that a person who is age 65 has a probability of having cancer equal to
0.5%1%0.2%2.5%
It may come as a surprise that even though being 65 years old increases the risk of having cancer, that person’s probability of having cancer is still fairly low. This is because the base rate of cancer (regardless of age) is low. This illustrates both the importance of base rate, as well as that it is commonly neglected.[3] Base rate neglect leads to serious misinterpretation of statistics; therefore, special care should be taken to avoid such mistakes. Becoming familiar with Bayes’ theorem is one way to combat the natural tendency to neglect base rates.
Problems using Bayes’ Theorem are often more easily grasped by applying the conditions given in the problem to a large pool of observations. Assume, for example, that a community consists of 100,000 people. According to the statement of the problem, 1% of the population, or 1,000 people will have cancer. 0.2% of the population, or 200 people, will be 65 years old. Of the 1000 people with cancer, only .5%, or 5 people, will be 65 years old. Thus, of the 200 people who are 65, only 5 can be expected to have cancer. 5/200 = 2.5%
Abuse
Now comes the fun part, abusing it.
We have people using this statistical tool to work out the probability of historical events, and so here are a few examples.
- William Lane Craig, the conservative Christian apologist, uses Bayes Theorem to “prove” that Jesus actually did rise from the dead.
- Richard Carrier, uses Bayes Theorem to “prove” that Jesus didn’t exist at all.
Clearly something is very very wrong here because Bayes Theorem has established two mutually exclusive conclusions as true. How can Jesus not actually exist at all and at the same time have actually risen from the dead?
What is wrong here is that Bayes Theorem is not being used correctly by either Craig or Carrier and is instead being grossly abused.
How many historians, apart from Carrier, use Bayes Theorem to establish the probability of any historical events?
None that I’m aware of, and there is a reason for that.
That reason is not because they are mathematically illiterate but rather is a reflection of the fact that a tool such as this will only function in a meaningful way if you have hard solid data to plug into it. If, for example you wished to determine the probability of something happening, then you can use cold hard facts such as how often has it happened before and with what frequency it has happened before.
If however you are trying to work out the probability of some historical event and you don’t have any facts, just assumptions, then you are stuffed because plugging in assumptions will lead to a meaningless measurement of the probability of the thing you are trying to determine.
What about those questions
OK, my intent was not to examine the Jesus question, but for the sake of completeness, let’s briefly examine that a bit.
Evidence that he rose from the dead is exactly zero. It is just a religious belief.
It is highly probable that Jesus did exist. The general consensus amongst historians (and I’m not talking about religious ones) is that a real human resides under the layers of supernaturalism and religious beliefs. A similar example is that Joseph Smith was also quite real historically, but the claims asserted by him and by the Mormon church are not factual.
The primary point here is this. Bayes Theorem can be used but also abused. If faced with somebody touting sciency sounding maths as proof regarding something, then don’t just roll with it, because the concluson being promoted will only be as good as the raw foundational data itself, and if that is itself dubious, then you can be sure that the conclusion is as well. The story of Rumpelstiltskin weaving gold from straw is myth, but apparently that has not stopped others from giving it a go.

I agree Bayes theorem gives a meaningless result if you don’t know the inputs. You are not in that situation however! In your last paragraph you say “Evidence that he rose from the dead is exactly zero”. That means P(E) = 0. From that it simply follows that P(H|E) = 0 so long as the denominator P(E|H) is non zero. The fact that P(E|H) is non zero is uncontroversial, i.e the probability that the gospel writers and Paul would report the resurrection if it happened > 0. Even if it’s vanishingly small, e.g 0.00000001 it doesn’t matter, you still get P(H|E) = exactly zero.
Furthermore, if we don’t know the inputs, then we can’t know the probability of the resurrection at via any other method. Bayes theorem gives the exact result. Appealing to intuition or measuring frequencies is just using heuristics which approximate the exact result given by Bayes theorem. It makes no sense for someone to say “the resurrection didn’t happen” (P(H|E)=0), but also say “we can’t calculate the result of Bayes theorem” (P(H|E)=?). That’s just a mathematical contradiction. Not that you’re saying that necessarily, but I just wanted to point that out.
The fact that people believe something is not “evidence” that it actually happened.
People did indeed once sincerely believe in Thor and Zeus. People did indeed once sincerely believe the sun was a God. You don’t need to seriously consider any of these as viable or that the existence of such a sincerely held belief in the past is in any shape or form “evidence” of an actual reality.
The problem you face is that you can do what you are doing with almost any sincerely held belief and reach conclusions that are simply not rational.
As the old saying goes when considering such algorithms – GIGO (Garbage in, Garbage Out).
I should add that I recognise that you do sincerely believe it to be true. This however is not the reason you have for holding that belief, it did not persuade you, and neither does it persuade me.